The 2014/15 El Niño – Part 1 – The Initial Processes of the El Niño

The title of the post, of course, assumes that an El Niño event will form this year and carry over into the next.

This post is intended for persons new to the topic of El Niño events—and for those who are familiar with them. It should help provide a number of different perspectives on the evolution of an El Niño and supplement our earlier post An Illustrated Introduction to the Basic Processes that Drive El Niño and La Niña Events.

For this post, we’ll primarily be discussing animations of data maps and subsurface cross sections from the NOAA Global Ocean Data Assimilation System (GODAS) website.  We’ll also be looking at subsurface temperatures and anomalies from a couple of ECMWF reanalyses.  Because there are a number of gif animations, the post may take a few moments to download.  Also, you may need to click start the animations, especially if you’d like a closer view.

LOTS GOING ON BELOW THE SURFACE OF THE TROPICAL PACIFIC

If we look at an animation of NOAA GODAS sea surface temperature anomaly maps (Reynolds OI.v2 data), starting in January 2014 and produced at 5-day intervals, we’d be hard-pressed to tell that a moderate to strong El Niño event may be evolving. See the left-hand maps in Animation 1. But when we look at the (right-hand) maps of the subsurface temperature anomalies for the depths of 0-300 meters, we can see that something is happening below the surface. That something, traveling eastward along the equator, has caused subsurface temperature anomalies to increase.   That something is called a downwelling Kelvin wave. And, yes, that’s Kelvin wave as in Lord Kelvin.

Animation 1

Kelvin waves along the equatorial Pacific come in two flavors: downwelling (warm) Kelvin waves and upwelling (cool) Kelvin waves.   The downwelling and upwelling Kelvin waves generally alternate. The “warm” Kelvin waves are called downwelling because they push the thermocline down, and the opposite holds true for “cool” upwelling Kelvin waves. (I’ll discuss the thermocline is a few moments.) Figure 1 is a Hovmoller diagram from the NOAA weekly ENSO update dated March 31, 2014. (See their page 16.) Don’t be intimidated by the Hovmoller. It is a wonderful way to present data. The left-hand (y) axis is time (a year), with the most recent week at the bottom. The bottom (x) axis presents the longitudes of the equatorial Pacific. South America would be to the right and Indonesia to the left. The subsurface temperature anomalies (for the top 300 meters) are color-coded with warm anomalies in red and cool anomalies in blue.  The dashed lines highlight the (warm) downwelling Kelvin waves and the dotted lines highlight the (cool) upwelling Kelvin waves.   Since August of 2013, there have been 3 (warm) downwelling Kelvin waves and 2 (cool) upwelling Kelvin waves. The first two downwelling Kelvin waves in the Hovmoller were relatively weak, and they occurred a little late in the 2013 season, so they did not result in an El Niño event. The most recent downwelling Kelvin wave is a reasonably strong one, and it’s at the right time of the year, leading to the thoughts that a strong El Niño will form this year.

Figure 1

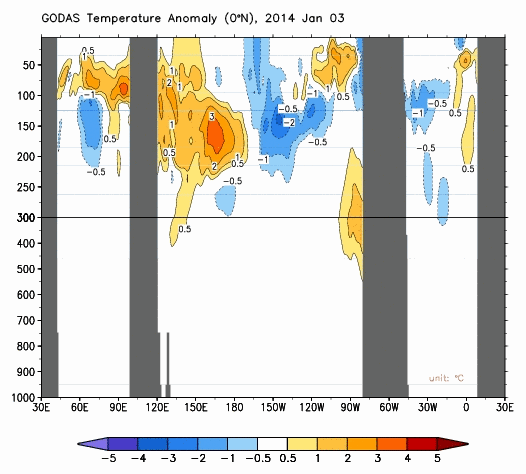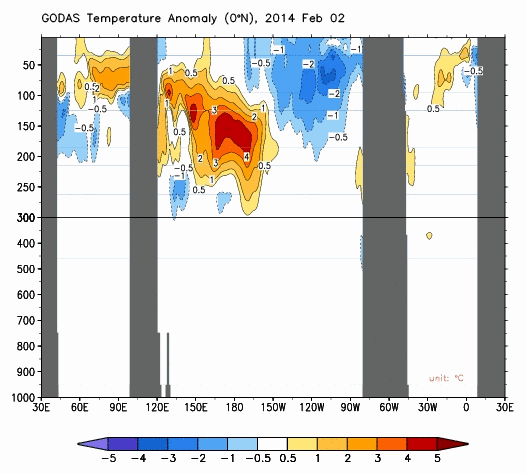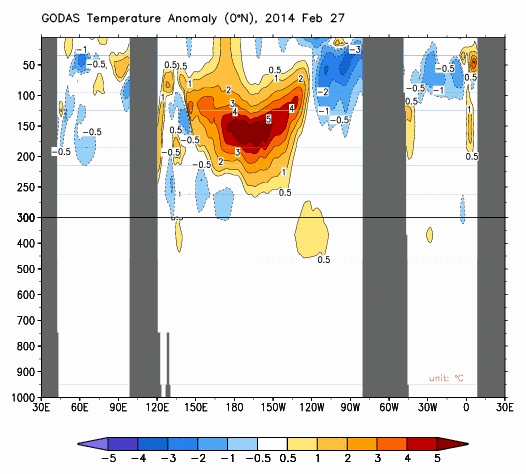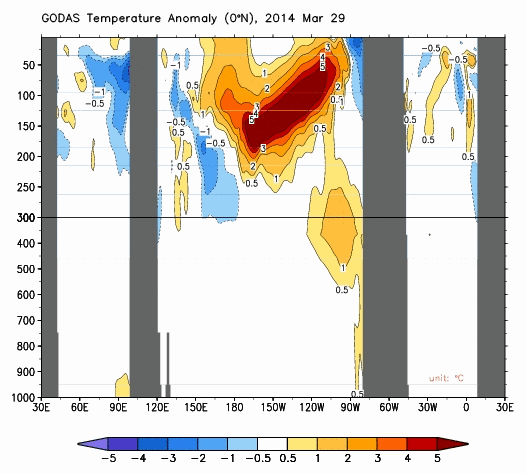
Cross sections of subsurface temperature anomalies along the equator are presented in Animation 2. From this perspective, it’s as if they sliced the Earth open at the equator and we’re viewing the temperature anomalies of the equator below the surface, looking toward the north. Again, these cross sections are available from the NOAA GODAS website. The Pacific is in the center cross section (with the Indian Ocean to the left, and the Atlantic to the right). The vertical axis is depth. The vast majority of El Niño- and La Niña-related processes take place in the top 300 meters (984 feet). Also keep in mind that the Pacific stretches more than 17,000 km (about 11,000 miles), almost halfway around the globe, at the equator. In other words, the distances and depths are not proportional in those cross sections and can’t be if they’re going to be informative.

Animation 2

Notice how the subsurface temperature anomalies grow stronger along the equatorial Pacific as the Kelvin wave travels east. That’s because the climatology (the average reference temperatures from which the anomalies are calculated) has cooler temperatures in the eastern equatorial Pacific. As an example, see the annual GODAS climatology for those subsurface temperatures in Figure 2.

Figure 2

I was hoping to animate the Kelvin wave working its way east using absolute temperatures, not anomalies, just to give you a better idea of what’s taking place. Unfortunately, as far as I know, GODAS only has cross sections using anomalies; that is, they do not also present the subsurface temperatures in absolute form. And the latest month of the ECMWF ORA-S4 Reanalysis is February 2014, so that wouldn’t be very helpful to us now.

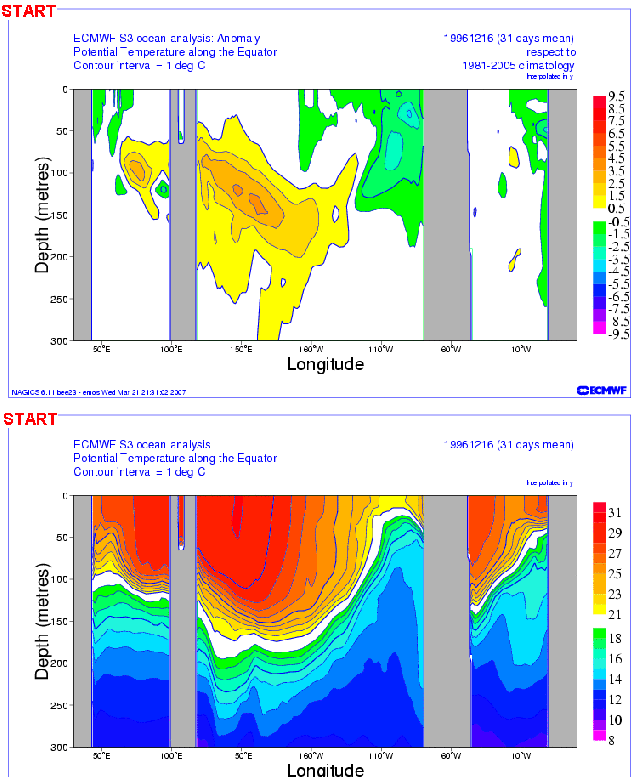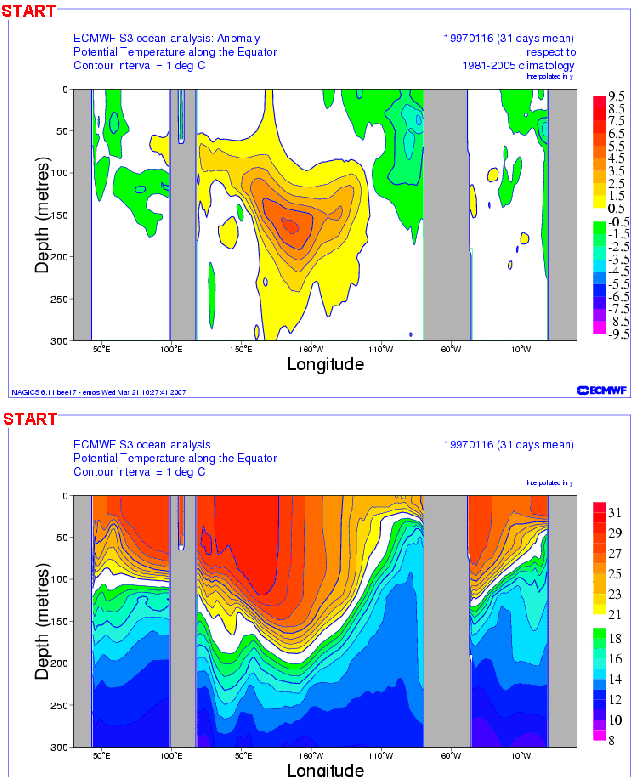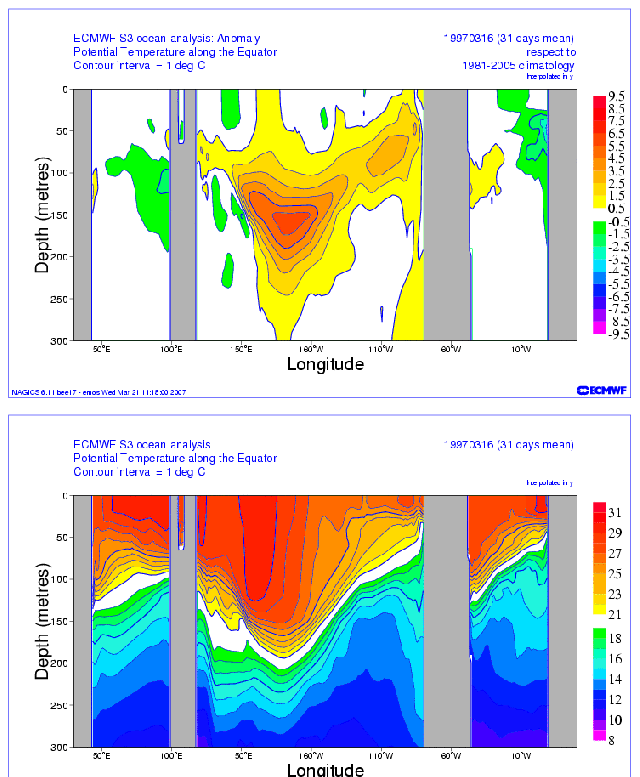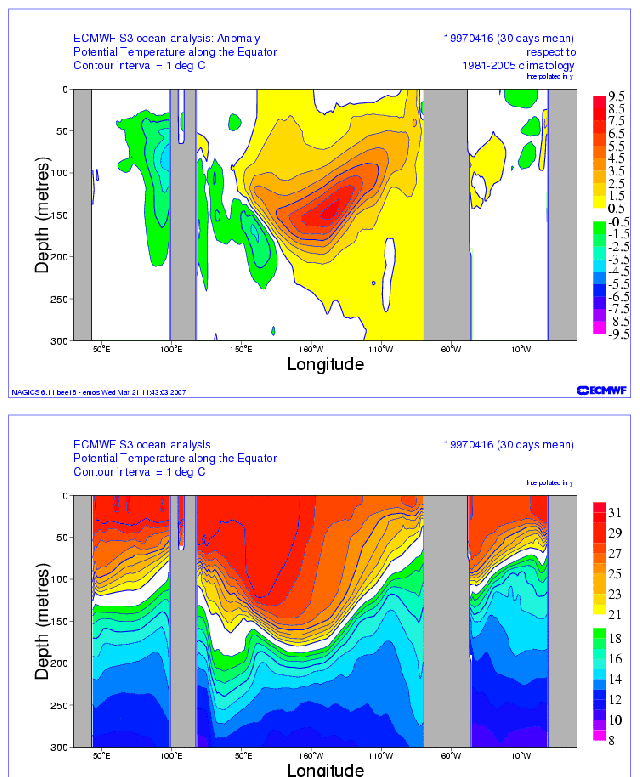
Luckily, somewhere along the line, I created an animation of subsurface temperature data (anomalies and in absolute form) of the 1997/98 El Niño, using cross sections available from an earlier ECMW reanalysis. Animation 3 presents the ECMWF subsurface cross sections from December 1996 to April 1997 as anomalies (top cell) and in absolute form (bottom cell). This is just a small portion of the original animation.

Animation 3

We can see the anomalies working their way eastward in the top cell of Animation 3 as the Kelvin wave(s) travels east. (See the note below.) In the bottom cell of Animation 3, we can see how the Kelvin waves depress the thermocline, as they travel east. I suspect the little rebound we see halfway through in the lower cell occurred between the 2 Kelvin waves.

Note: There were actually 2 downwelling Kelvin waves that preceded the 1997/98 El Niño. See the portion of a JPL sea level residual animation here. The first downwelling Kelvin wave that started around Christmas of 1996 appears to have had little effect, but the second one a couple of months later definitely started the ball rolling. [End of Note.]

Recall earlier that we noted that a downwelling (warm) Kelvin wave pushes down on the thermocline. The thermocline is the boundary between the mixed waters (nearer the surface) and deep ocean waters. The thermocline (20 deg C) is highlighted in white in the lower cells of Animation 3.

WHAT INITIATED THE KELVIN WAVE THIS YEAR?

We recently discussed Westerly Wind Bursts in the post ENSO Basics: Westerly Wind Bursts Initiate an El Niño. The start of the 2014/15 El Niño (assuming it continues to form) is another classic example. See Figure 3. Two apparent westerly wind burst-like shifts in the zonal (east to west) winds can be seen in the left-hand Hovmoller diagram from GODAS.   That is, the trade winds, which normally blow from east to west, suddenly and temporarily shifted to westerlies, blowing from west to east. I’m sure someone will eventually explain in a paper what weather event caused the westerly wind bursts.

Figure 3

THE KELVIN WAVE ISN’T VERY HIGH BUT IT SURE IS LONG

Without the magic of satellite altimetry, it would be impossible to sense the equatorial Kelvin wave as it traverses the Pacific from west to east. It’s incredibly long, but not very high. In Animation 4, the GODAS maps of sea level anomalies are on the left, and the maps of subsurface temperature anomalies for the top 300 meters are on the right.

Animation 4

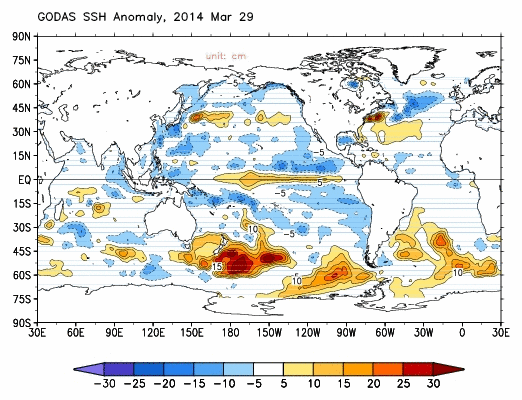
As of March 29, the sea level anomalies map (Figure 4) is showing a positive anomaly of between 10 and 15 cm (about 4 to 6 inches) at the greatest contour levels along the Kelvin wave, and based on the 5 cm contour line, it stretches from about 165E to about 95W or about 11000 km (about 6900 miles). (See the NOAA Latitude-Longitude Distance Calculator.)

Figure 4

The processes taking place in the Pacific when an El Niño develops are enormous in scale.

AN INTERESTING PERSPECTIVE FROM ECMWF

The ECMWF ORA-S4 reanalysis also presents cross sections of average subsurface temperatures but on what they call a “YZ” perspective, which is as if they took large slices of the Pacific ocean running south to north and we’re viewing the average temperatures and anomalies facing west. Figure 5 shows the west and east Pacific coordinates they’re illustrating in the YZ plots.

Figure 5

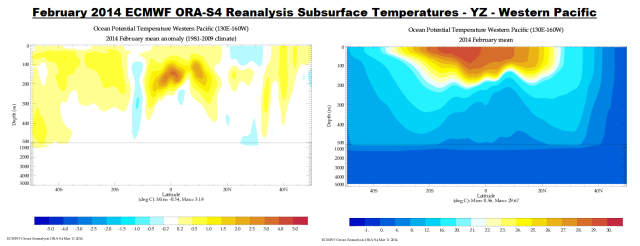
The February 2014 reanalysis of the West Pacific (50S-50N, 130E-160W) subsurface temperature anomalies (left) and subsurface temperatures (right) are shown in Figure 6. South is to the left, north to the right and the equator is in the middle. The vertical axis is depth. The temperature scales are below each plot. The positive subsurface temperature anomalies associated with the downwelling Kelvin wave appear below the equator in the left-hand cell. The pocket of positive anomalies below the surface at about 10N should be the remnants of the downwelling Rossby wave returning the warm water to the west from an earlier downwelling Kelvin wave. I’ve included the plot of absolute temperatures on the right simply to put things in perspective.

Figure 6

The East Pacific (50S-50N, 160W-90W) subsurface temperature anomalies (left) and subsurface temperatures (right) for February 2014 are shown in Figure 7. The Kelvin wave hadn’t made it far enough to the east in February to make its presence known in these plots. In the right-hand cell of Figure 7, note how the warmer water does not reach as deep in the eastern Pacific as it does in the western Pacific shown in Figure 6. The trade winds push the warm water to the west where it “piles up”. The trade winds also help to draw cool water to the surface along the equator in the eastern Pacific in a process called upwelling.

Figure 7

NINO3.4 REGION SEA SURFACE TEMPERATURE UPDATE

The NINO3.4 region is bordered by the coordinates of 5S-5N, 170W-120W. See the illustration here for the location. The sea surface temperature anomalies there are a commonly used index for the strength (how warm or cool), frequency (how often they occur) and duration (how long they last) of El Niño and La Niña events. Based on the weekly Reynolds OI.v2 data for the week centered on April 2, 2014, the NINO3.4 sea surface temperature anomalies are presently at +0.38 deg C, which is below the +0.5 deg C threshold of El Niño conditions. See Figure 8.

Figure 8

Figure 8 is from the (most recent) March 2014 sea surface temperature anomaly update.

Hopefully, this post has helped to show how ridiculous it is to think that an ENSO index represents the processes of ENSO.

FUTURE POSTS

I’ll be updating the animations in future posts. I’ve downloaded the maps and cross sections so that I can add on the new ones to the ends of what has already been presented. (GODAS only animates for 3 months.) That way we can track the warm water, and continue to follow it during the La Niña that’s sure to follow.

I don’t believe I can establish a schedule for these posts. But I will update when something interesting happens that will help confirm the processes of El Niño discussed in An Illustrated Introduction to the Basic Processes that Drive El Niño and La Niña Events. Maybe I’ll prepare the next one when the NINO3.4 sea surface temperature anomalies cross the threshold of an El Niño and reach a reasonably warm value and when the trade winds in the western tropical Pacific reverse and become westerlies.   We’ll see what happens.

Please feel free to suggest/request topics for upcoming posts.

ADDITIONAL READING

I went into much more detail to explain ENSO processes and the aftereffects of El Niño and La Niña events in my ebook Who Turned on the Heat?  I’ve lowered the price of Who Turned on the Heat? from U.S.$8.00 to U.S.$5.00…with hope of increasing sales a little bit.  A free preview in pdf format is here.  The preview includes the Table of Contents, the Introduction, the first half of section 1 (which was provided complete in this post), a discussion of the cover, and the Closing. Take a run through the Table of Contents.  It is a very-detailed and well-illustrated book—using data from the real world, not models of a virtual world. Who Turned on the Heat? is only available in pdf format…and will only be available in that format.  Click here to purchase a copy.  Thanks.

CLOSING COMMENT

It is unfortunate that NOAA budget cuts have resulted in reduced operation of the Tropical Ocean-Atmosphere (TOA) Project array of moored El Nino-monitoring buoys. See the Nature editorial Support our buoys. I understand from a follow-up Nature article El Niño tests forecasters that NOAA has “committed” to having most of the system operational by the end of the year, but, unfortunately, by that time, the El Niño will be near or at its peak intensity. I find it quite remarkable that federal budget cuts have caused the partial demise of such an important system. The array should not have been left to decay; it should be expanded to cover the entire tropical Pacific, not just the latitudes of 10S-10N, because El Niño- and La Niña-related processes take place within the tropical Pacific but outside of the latitudes presently being monitored by the TAO project. NOAA should be increasing, not decreasing, the budget of the Pacific Marine Environment Laboratory.